by Chatzichri’stos Aris
Department of Electrical and Computer Engineering,
National Technical University of Athens (NTUA), Athens, Greece.
Contents
Abstract
Introduction
1. Basic Concepts and Principles
2. Conservation of Energy
3. Entropy and Space Expansion
4. Destination and Velocity
4.1 Movement
4.2 Destination
4.3 Velocity
5. Newtonian Gravitation and Special Relativity
5.1 Gravitational Force
5.2 Special Relativity
6. General Relativity and Dark Matter
6.1 General Relativity
6.2 Dark Matter
7. Hubble’s Law and Dark Energy
8. Inflationary Universe
9. Observable Predictions
Conclusions
References
Abstract
Deduction of a quantum model, with basic principles the Discrete nature of Space and the Second Law of Thermodynamics, which is compatible with Special Relativity in the absence of Gravity, while its linear edition is proven to be compatible with linear General Relativity (aka the first order terms of the two theories are basically identical). Finally, is being proven that the non-linear edition of this theory contains the phenomena of Dark Matter and Energy as its natural conclusions. Also, some astronomical observations are proposed to test the theory.
Introduction
According to General Relativity[1][2], the mechanism of Gravitation is the curvature of space-time around massive bodies. This idea is exceptionally accurate at a macroscopic scale. Nevertheless, at a microscopic level it has been proven to be incompatible with the Standard Model of Quantum Mechanics. Therefore, it would be very useful for the pursuit of the unification of these two theories, if a model was to be found, that could be proven equivalent to the curvature of space-time, but without these characteristics that make Relativity incompatible with the theories of Quantum Mechanics.
Moreover, a theory of Quantum Gravity should explain the phenomena of Dark Matter and Energy. According to the established theories, the expansion of the Universe was caused by the Big Bang and the total Gravitation of the Universe should slow it down. On the contrary, the astronomical observations of the last decade[3][4] prove that in fact this expansion accelerates. For the solution of this paradox, it has been assumed that the Universe is almost completely dominated by Dark Energy[5], a sort of exotic anti-gravitation of empty Space, which cancels the effects of normal Gravitation and thus accelerates the expansion of space-time. The nature of this Energy remains a mystery.
In addition to the above stated problem, other astronomical observations imply that the total known mass of the galaxies is not enough for them to be stable and produce the extensive gravitational halos that are observed throughout the Universe. This unknown missing mass is named Dark Matter[6].
The goal of this paper is to propose a theory that can explain the above phenomena. The point of view of this proposed model is close to “Loop Quantum Gravity”[7][8], but with some crucial differences: On the one hand space is quantized, just like in LQG. But on the other hand there is no actual curvature. Space is discrete, but flat. All the phenomena that have to do with gravitation and the supposed curvature of space-time are being created by a different (but at the end equivalent) mechanism: The creation of new space around massive bodies.
Let’s enlighten this mechanism by using the following Gedank experiment:
Let two points A and B; between them there is a “moving walkway”, like the ones that exist in every gym. When this walkway is “off”, it does not move and then an observer, starting from point A at some moment, calculates the amplitude of AB by moving with constant velocity from A to B and thus counting the time needed. Then obviously,
|AB|=u·t
Now, if the moving walkway runs with a constant velocity, smaller and opposite to the velocity u of the observer, then if he/she moves from A to B with the same velocity as before, this observer will calculate a bigger value for the |AB|. Thus, one can argue that at the second occasion the line segment AB has been curved.
One can say that when the moving walkway is on, then at the point B “new space” is created, which moves afterwards in the opposite direction of the movement of the observer.
Intuitively, one can argue that if massive bodies produce new space, which moves afterwards away from them, then perhaps this procedure can create a phenomenon that looks much alike a moving walkway and is equivalent to the curvature of space-time around masses.
Thus, the basic compass–question of this paper will be the following: Could the gravitational expansion of a given length (curvature) have a closer connection to the expansion of the Universe?
Let us make the last thought more specific:
Gravity is a Force, so it should be connected to a particle. If Gravity is produced by the expansion of space, then one concludes that space should be discrete. That will be the basic hypothesis, from which this theory of Quantum Gravity will be deduced. Empty space can be regarded as the particle with the smallest possible energy; therefore the energy of empty space is quantized too. We name this energy “quantum of energy”. In this model, quantum of energy can be consider as the sole “elementary particle” in the sense that all other particles, including space, are systems of quanta of energy.
When the Universe expands, new quanta of space should be created and thus, due to the Principle of Conservation of Energy, an equal amount of energy should be consumed somewhere. The source of this energy is obviously the massive bodies and the photons, i.e. the objects that contain energy. This means that new space is being created around great structures of mass and then is moving “outwards”. As a result, an observer stationed near a mass, notes the expansion of a given length, as light has to travel through this moving space, in addition to the classical constant space. The situation is much alike a three dimensional gym walkway, on which light , while moving with a constant velocity, needs more time in order to travel a given length, when a massive body is around.
One might wonder how space can possibly be discrete without being observed so far. The answer is of course the order of magnitude. After all, mass is also discrete, but this fact is obvious only in scales of about 10-14m. The proposed quantum of space is expected to be much smaller. It is likely, for example, to be equal to Plank’s length. As this is of the order of 10-35m, it can easily be understood why one cannot observe directly the discrete nature of Space.
This paper studies gravitation, using the above considerations. It accomplishes the following:
1) The construction of a “grid” of quanta of space (similar to the “spin network” of Loop Quantum Gravity).
2) The deduction of space expansion using only the Second Law of Thermodynamics in this space.
3) The finding of Special Relativity, using only discrete mathematics and considerations similar to those of Zeno of Elea.
4) The proof that the solution for the point-like source of gravity in this discrete space is completely equivalent to the Schwarzschild solution.
5) The explanation of Dark Matter and Energy, without asking for other exotic structures. Not even a cosmological constant.
6) The Inflationary era: Why it started and why it ended.
7) The proposal of some possible experiments and observations for the test of the theory.
1. Basic Concepts and Principles
If one accepts the basic principle of the Discrete nature of Space, as it follows from the introduction, then one should first of all solve the problem of the topology of such a Space. As space is made of particles, this problem is identical to the basic problem of crystallography, with the obvious replace of atoms with quanta of space. Thus, we will search for a similar solution:
[1.1] First of all, let an infinite mathematical grid. Like all grids, its edges (or nodes) are countably infinite and therefore they can be defined by a vector with integer coordinates. As this grid is mathematical, it does not exist physically, it is considered merely as a base for the formalism and the better understanding of the theory. Thus, its existence will not be inserted axiomatically. However, the number of dimensions of this grid is important to the Universe itself; therefore one must accept the following postulate:
1st Axiom: The grid is 3-dimentional.
(Dimensional Principle)
[1.2] That grid should satisfy some obvious crystallographic prerequisites:
- First of all, the geometry of its fundamental cell should allow the covering of the entire infinite mathematical space with such cells.
- Second of all, at every direction the fundamental cell should be unitary, so all directions to be equivalent even in the smallest possible scale.
[1.3] With the above prerequisites in mind, one can search in the theory of crystallography[9][10], to find which structures are compatible. In 3D there is only one compatible topology, the one in which every node is connected with 6 others, in a structure of a 3-dimentional cross (Figure 1). At the elegant language of Bravais grids, the fundamental cell of this space is simple cubic (sc).

Figure 1: The unitary and the fundamental cell of Space
Definition 1.1: Unitary distance (quantum of distance) is the distance between the center and any other node of the same unitary cell.
Definition 1.2: When two nodes are at a unitary distance, then they are neighbors.
Definition 1.3: We define the distance of two random nodes of the grid to be the minimum number of neighboring points, from which one should pass in order to go from the first node to the second.
[1.4] It is quite obvious, that on this background it is not possible to use the Euclid’s norm in order to define distance, as the expression
![]()
might not be an integer and therefore cannot be accepted. As a result, the norm ||r||1 = |r1|+|r2|+…+|rn| will be preferred for the definition of the amplitude of the vectors that will be used. This norm can always be defined in a discrete space, as it gives a natural number for integer coordinates.
[1.5] One should bear in mind that these two norms are mathematically equivalent. As a consequence, for large numbers, when the discrete nature of space can be neglected, one can use with an excellent approximation Euclid’s norm.
[1.6] The distance of two points of the grid with coordinates r1=(a1,b1,c1) and r2=(a2,b2,c2) is: |r|=|r1-r2|= |a1-a2|+|b1-b2|+|c1-c2|. Of course distance cannot acquire negative values.
[1.7] One can study in dept the problem of the geometry of the grid, but in this paper the only results that will be needed is the number of nodes at given distance r (where r natural number) from a constant node and the number of nodes inside that radius. For them in can be proven (with mathematical induction) that:
![]()
[1.8] Equations 1 and 2 reflect respectively the number of solutions of the Diophantic equation and inequality:
|x-xo|+|y-yo|+|z-zo|=r and |x-xo|+|y-yo|+|z-zo|≤r
Where (xo,yo,zo) is the point of reference.
[1.9] With this grid as background, one can put on it some elementary objects, the quanta of energy. These are fully defined by their position on the grid (vector of position) and by their destination point (vector of destination). Those objects are “real”, therefore their existence should be demanded axiomatically:
2nd Axiom: There is a finite number of discrete objects, named “quanta of energy”. From a mathematical point of view, every one of them can be defined by a matrix, which contains two vectors: One for its position and one for its “destination”.
(Principle of Definition of Energy)
In the following chapter the concept of “destination” will be used in order to define velocity.
[1.10] One might wonder about the necessity of the concept of “destination”. In the continuum space of the established theories there is not such a need, as one can define the movement of the various particles by the velocity vector. However, in a discrete Space this idea is preferred, for reasons that will become clear later in this paper.
Definition 1.4: If there is only one quantum of energy that has a particular vector of position and its vector of position is identical to its vector of destination, then it is called quantum of space.
I.e., a non-moving particle of unitary energy is space.
Definition 1.5: The set of all quanta of space is called volume of the Universe.
Definition 1.6: If at the same point with a quantum of space co-exist another one quantum of energy, which vectors of position and destination are in general different, then this quantum of energy is called quantum of gravity, or graviton.
The quantum of gravity can be considered to be moving new space.
Definition 1.7: If at the same point with a quantum of space there is also a number of quanta of energy (more than one) then all these quanta, except for the quantum of space, are called photon.
Definition 1.8: A point of the grid that is not covered by a quantum of space is called a hole.
[1.11] From the above definitions mass shines by its own absence. One could observe that in a discrete space, all particles must be systems of elementary particles of volume equal to one quantum of space. It can be proven that all particles with mass are stable structures of interactive photons[11]. However, the details of this interaction are not connected directly with gravitation; therefore we will not deal with this hint in this paper. Here, the existence of massive structures will just be a valid hypothesis.
2. Conservation of Energy
3rd Axiom: The number of all quanta of energy of the Universe is constant. (Principle of Conservation of Energy)
[2.1] According to the above definitions (1.4-1.7) the Principle of Conservation of Energy can be written equivalently as:
Εγ+Β+V=E=constant. Eq. 3
Where Εγ is the total energy of all photons of the Universe expressed in quanta of energy, B is the total number of quanta of gravity and V the number of all quanta of space (volume) of the Universe.
[2.2] The Principle of Conservation of Energy does not forbid transformations of energy of photons into quanta of gravity or space. Also, it does not forbid the opposite procedure. However, with the next axiom it will be forbidden for a quantum of space to transform into something else, therefore their numbers should increase constantly.
3. Entropy and Space Expansion
Definition 3.1: Entropy[12] is defined by:
![]()
Where E is the total energy of the Universe, Ei is the amount of quanta of energy with a particular vector of position and Ε1+Ε2+…+Εn=Ε (from the Principle of Conservation of Energy).
4th Axiom: The Entropy of the Universe increases constantly.
(Second Law of Thermodynamics)
Theorem 1: The fourth axiom (SLT) is equivalent to the expansion of the Universe.
[3.1] Proof:
In order for Entropy to increase, the denominator of the logarithm of Eq. 4 should decline (the numerator is by axiom 3 constant).
When at a point of the grid there is only one quantum of energy (i.e. a quantum of space) then this particle does not contribute to the product of the denominator, as it has energy 1 and so Ei!=1. Also, when a high energy photon breaks into two lighter photons, then the entropy of the Universe increases, as (Ε1+Ε2)!>Ε1!+Ε2!.
In conclusion, the constant amount of quanta of energy should be distributed into an always increasing number of particles with different vectors of position. The final consequence of this distribution is that at the end all quanta of energy will become quanta of space; thus Entropy will be maximum.
If someone goes backwards in time, the decline of Entropy leads by induction to the conclusion that at a distant moment in the past, all quanta of energy must have been part of only one photon (Big Bang). If one associates the quantum of space with Plank volume, then one can possibly explain why Universe at the time of the Big Bang might had volume equal to Plank’s.
In reverse: If the volume of the Universe increases, then a part of the energy of particles should become quanta of space, which do not contribute to the denominator of the logarithm. Thus, Entropy increases with time. Q.E.D.
[3.2] A natural consequence of the above theorem is that a quantum of space cannot transform into something else, as that action would decrease the Entropy of the Universe.
[3.3] Increase of Entropy and the Expansion of the Universe are equivalent (theorem 1.1). However, Entropy increases every time two or more particles construct a system (i.e. every time they interact). Thus, the increase of Entropy cannot be caused by the expansion of the Universe, but (as they are equivalent) the expansion of the Universe should be caused by the increase of Entropy. Consequently, every time two particles interact, new space should be created.
[3.4] One might argue, that the above discussion about the expansion of the Universe supports an open Universe, with well defined limits. However, this is in contrast with the established opinion. Nevertheless, at chapter 8 it will be proven that the above type of expansion is not directly observable at nowadays Universe, but it was dominant at the early Universe. In other words, it will be proven that this type of expansion has to do with the Inflationary Universe. The expansion of today’s Universe is due to a phenomenon that is produced by the above analyzed expansion mechanism, but is also compatible with the established models of the Universe.
4. Destination and Velocity
4.1. Movement
[4.1] The following question arises: How the quanta of energy move from a point A to another node B, at distance r from A?
Axiom 2 implies that the quanta of energy cannot follow a route with length more than r, in order to move from A to B. If that was possible, then nothing would stop this length to be as large as it wants, even infinite. But then the steps of the quantum might as well be arbitrary. In that case it would not be meaningful to say that this quantum is moving from A to B at all, therefore the concept of destination would also be meaningless. However, that is in contrast to axiom 2. Consequently, the quanta of energy should follow one of the alternative routes of minimum length, in order to move from A to B (Figure 2).
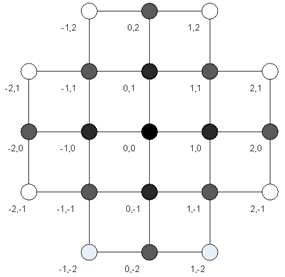
Figure 2: A 2-D representation of the grid. If a body is to move from Α=(0,0) to Β=(2,1), it can follow one of the following routes of minimum length:
(0,0)->(1,0)->(2,0)->(2,1)
(0,0)->(1,0)->(1,1)->(2,1)
(0,0)->(0,1)->(1,1)->(2,1)
[4.2] The above analysis does not exclude the opposite case: A quantum of energy to move from A to B by passing by less than r nodes: Could it, for example, teleport from A to B, regardless of their distance, or move from A to B by passing from every two nodes in its way? The answer is no. If a body can transport directly from a point to another, then these points are, by definition 1.2, neighbors. Thus these points should belong to the same unitary cell of the grid. But if two random points of space belong to the same cell, then all points of Space should belong to the same cell. But, from crystallography it follows that this is impossible. With the prerequisites of [1.2], every point can have only six other neighboring nodes. Consequently, the quantum of energy cannot move from A to B with less than r steps.
[4.3] From paragraphs [4.1] and [4.2] we have that a quantum of energy at the point A reaches B after exactly r steps.
4.2. Destination
[4.4] In general there are two ways to define a vector: By using its starting and ending points (like in classical Descartes’ analytical geometry) or by using an amplitude-angle formalism.
[4.5] If the ending point of the vector is at “infinity” then these two formalisms are basically identical. The particle will move forever in the same direction, with the same velocity. If the ending point of the vector is at a finite distance, then that particle at some moment will stop moving. One can see that the starting-ending point formalism is more general than amplitude-angle.
[4.6] In order for the Universe to expand, when a particle reaches a hole in the grid, it should stop moving (Def. 1.4). Thus, in this paper one needs a formalism that permits a particle to stop moving after travelling a finite distance. That is why the first formalism is preferred. Moreover, with this formalism it is easier to understand the phenomena of Dark Matter and Energy (see Chapter 6).
4.3 Velocity
Definition 4.1: The velocity vector of a quantum of energy is:
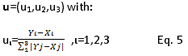
Where Υι-Χι is the distance at the i-axis of the destination point of the quantum of energy from the position of it.
[4.7] The velocity of a quantum of energy is normalized, i.e.
![]()
But
![]()
Thus, the quantum of energy makes every time a unitary “jump” towards its destination. That has been proven also at [4.3].
Definition 4.2: The time interval needed for this “jump” is called quantum of time and it is the minimum meaningful time interval.
Definition 4.3: The amplitude of the velocity of a quantum of energy is called speed of light.
It holds that |c|=1, unless it is a quantum of space, in which case its amplitude is zero.
[4.8] The various components of velocity are rational numbers with 0≤|ui|≤1 and they express the probability for the quantum of energy to move towards its destination at the i-axis at the next quantum of time.
Example 1.1:
The quantum of gravity with position vector r(t)=(1,1,1) and destination vector v=(1,2,6) has velocity u(t)=(0,1/6,5/6). At the next six quanta of time it will move 5 times towards the positive values of the third axis and one time towards the positive values of the second one. One cannot know a priori when it will move towards which axis, therefore this graviton has probability 1/6 to move at the next quantum of time towards the positive values of the second axis and probability 5/6 to move towards the positive values of the third axis.
If it moves during the next quantum of time towards the second axis, then its new position vector would be: r(t+1)=(1,2,1) and its new velocity u(t+1)= (0,0,5/5)=(0,0,1). Thus, at this case, from that point on it can only move towards the third axis.
[4.9] Paragraph [4.8] implies a non-deterministic structure at the core of the theory. Even at a most fundamental level, the exact knowledge of the future is impossible, even if one knows all vectors of position and destination of all quanta of energy in the Universe.
[4.10] At the example 1.1 the particle on-the-move was a quantum of gravity (1 quantum of energy). The case of the photon is slightly more complex, as one should consider all destination vectors of all quanta of energy of the photon. The photon must move with a resultant velocity of all its components, or else it would be teared apart very quickly. The study of this motion is out of the scopes of this paper.
5. Newtonian Gravitation and Special Relativity
5.1 Gravitational Force
[5.1] Theorem 1 basically states that the increase of Entropy expands Space. Entropy increases when two or more bodies interact. Therefore, new space is constantly being produced by massive bodies (as these bodies are either way systems of more simple structures), as well as every time a photon interacts with a quantum of gravity.
[5.2] Space contains some energy (one quantum of energy), so during the above stated interactions masses and photons should lose a quantum of energy. This is, of course, the mechanism of light’s red shifting. Light loses energy while inside a gravitational field (due to the increase of Entropy caused by its interaction with the quanta of gravity) which eventually becomes new space.
[5.3] Around massive bodies, holes in the grid of the quanta of space are not to be expected. If such a hole existed, a quantum of gravity would have filled it long ago. As a consequence, the new quanta of space produced by an interaction should propagate as particles on the already existed space, until they reach a hole in the grid. These particles are moving quanta of space; therefore they are by definition quanta of gravity. Consequently, the increase of entropy produces quanta of gravity.
[5.4] The quanta of gravity being produced by a given source must move radially outwards, because near the sources of gravity there are no holes. While moving away from their source, they might once in a while pass “under” a body. As quanta of gravity are basically moving space, by moving under a body they would have the same influence to that body as if “a carpet was pulled under the feet” of that body. So, this body, due to inertia, will move on the opposite direction of the movement of the new space. That means, it will move towards the source of the quanta of gravity. As a result, gravity acts always attractively.
[5.5] One can reach the above conclusion and by using Special Relativity. The compatibility of this theory with Special Relativity will be proven in the next chapter, but if one assumes it (for now without a proof), then one could conduct the following mental experiment: Let a body moving with constant velocity υ in respect to Space. If at a given moment a quantum of gravity passes “under” it, then, from the point of view of that body, Space instantaneously acquires a velocity, or equivalently, Space remains constant and the velocity of the body increases instantaneously. Therefore, the body accelerates.
[5.6] The probability of a body to be attracted by a source of gravity, due to the mechanism described in [5.5], depends on the density of the quanta of gravity. If the source of gravity produces a constant rate of quanta of gravity, which then move with the speed of light radially away from it, then the same number of gravitons will be spread in an ever increasing surface of a sphere. The area of this surface is 4πr2, consequently the density of the quanta of energy, thus also the strength of gravity, will be decreased with the square of the distance between the source and the body.
[5.7] At the paragraph [6.7] will be proven that the number of quanta of gravity a source produces is proportional to the mass of the source.
[5.8] Combining all the above results of this chapter, one can write down the classical Newton’s Universal Law of Gravitation.
5.2. Special Relativity
Before discussing about Gravitation, one should clarify the relation of this theory with Special Relativity. For this purpose the two axioms of Special Relativity are being stated:
1st Postulate of Special Relativity: All observers that move uniformly and without rotations with respect to the others describe nature with the same exactly laws.
Practically, this axiom states that there is no preferred system of coordinates.
2nd Postulate of Special Relativity: All observers measure the same speed of light.
[5.9] One might think that the proposed axiomatic formalization of this theory is completely incompatible with Special Relativity, as it predicts the existence of a constant Space, which could very easily play the role of a preferred system of coordinates (ether) for the velocity of the moving bodies. That is partially correct. Indeed, as follows from the first chapter, all vectors of position and destination (therefore also that of velocity) of the photons are always expressed in a system of coordinates which does not move in respect to Space.
[5.10] But this quantized Space differs to that from the imaginary ether of Maxwell: Even though they are both means in which the E/M waves (photons) are being propagated, the velocity of an observer in respect to the (by definition constant) quanta of space, is not directly observable. Observers do not interact directly with the quanta of space, only with other bodies that contain energy. If an observer wanted to measure his absolute velocity in respect to Space, he should compare it to that of a body that is not moving in respect to Space. But the knowledge of the absolute velocity of another body is transcendent; consequently the same is also true about the expression of the velocity of an observer in respect to Space.
In conclusion, the first axiom of Special Relativity is being satisfied by this theory. Technically there is an absolute velocity, but it is not directly observable.
[5.11] It is interesting that the very idea of ether had been proposed during the 19th century, for no one could believe that a wave (the E/M in particular) could propagate in vacuum. All the other waves that the scientists of that era had already encountered on earth (sound, sea, earthquakes…) were signals (of energy) that propagate in means of the same essence with the waves: Sound is an oscillation of the particles of air and propagates in the air; a tsunami is an oscillation of the molecules of water end it propagates in water. So, it would be natural for an electromagnetic wave to propagate in a mean with the same physical essence with the signal, not in a different essence, i.e. the ether. In this theory, empty space is a particle of the same nature with photons: They are both made of quanta of energy. One could say that, both Einstein and Maxwell were correct: Light is being propagated in vacuum, i.e. on a layer of non-moving photons of unitary energy!
The answer to the second postulate of Special Relativity requires the analysis of the way that an observer interacts with the rest of the world.
[5.12] Massive observers interact with their environment with a sort of a radar: They send photons, which reflect on other bodies and then return back.
[5.13] If one knows the speed of light (in the unit system used in this paper c=1) and the time needed for light to reach the object and return back, one can calculate the distance of that object from the observer as follows:
Let τ be the time light needs to reach the object and return. Then the distance is:
![]()
[5.14] A second (massive) inertial observer will calculate this distance as the Lorenz transformations predict, if and only if these two random observers agree on the speed of light. Then both axioms of Special Relativity will be valid in this theory as well, and with arguments essentially identical to those of Einstein, one can deduce the macroscopic Lorenz transformations.
Note: In his analysis, Einstein used a continuum space. However, the discrete nature of Space is not a problem, as the massive observers have dimensions of several (dozens) of orders of magnitude bigger than the quantum of space. Therefore, Space can be considered macroscopically continuum without any significant error.
[5.15] Let’s examine the way two random inertial observers count the speed of light:
Let the first observer stand still, in respect to Space, without naturally having knowledge of that fact. This observer sends photons to be reflected by mirrors that exist in various directions at distance s from his position. These mirrors are not moving in his system of coordinates. Naturally, in all cases the photons will be reflected and return after time τ=2s, therefore this observer will conclude (using the formula of Radiolocation) that in all directions the speed of light is
![]()
Let the second observer be moving with a random velocity υ (<c) in respect to Space. This observer also calculates the speed of light the same way as before. The photon that moves towards the target in the direction of the velocity of the observer will reach that mirror after time τ1=τ+τ΄, where τ is the time needed for light to reach the point where the mirror was, at the time the photon was emitted and τ΄ is the time needed for the photon to reach the mirror from that point forward. Next, it will be reflected and start moving backwards. As the observer is moving with the same speed as the target, the photon will reach the observer after time τ2=τ-τ΄. Therefore, the total time of the trip of that photon will be τ1+τ2=2τ. So, the second observer will also conclude that c=1. The exact same analysis for the second observer is valid in any random direction, consequently these two random observers agree on the speed of light.
[5.16] Both axioms of Special Relativity are valid in this theory, so it follows that in a macroscopic level the Lorenz transformations hold. On the other hand, in a quantum level, where the distances are comparable to the quantum of space, then these transformations should undergo a slight change, as they contain the term
![]()
which can get transcendental values – which can naturally not be defined in a discrete space-time. The quantum Lorenz transformations should give rational numbers and be compatible with the classical transformations in macroscopic scales. Finally, one should set c=1 at the denominator of γ.
[5.17] As an example, we will construct the quantum Lorenz transformation, in the case that there is a stick of length L, which is still in respect to the first observer (A). Also, there is an inertially moving (in respect to A) second observer (B). According to the classical Lorenz transformations the second observer will measure the length of the stick to be
![]()
Let us examine those two observers in a quantum level:
Observer A, who stays at the center of the coordinates, counts the length of the stick, being along the x-axis, by emitting at the same moment two photons to be reflected at the opposite sides of the stick. As c=1, the length of the stick will be equal to the difference of the two returning times.
Observer B is moving with velocity υ along the x-axis. Let’s say that he is moving away from the stick. When the second photon is being reflected at the far side of the stick, the first photon precedes it by time equal to t=2L. This distance remains constant until the first photon reaches the moving observer B. The second photon will reach the point, where B was at the time of the return of the first photon, after time 2L, but in the meanwhile B will have travelled a distance 2Lυ. When the second photon has travelled this additional distance, the observer will have been moved by 2L·υ2, etc… The second photon will finally reach B, when the term 2Lυν<1. Then the photon will be less than a quantum of space away from B, therefore their positions will be identical.
If τ is the difference of the two return times, then the length L of the stick will be (according to the radiolocation formula) equal to:
![]()
If now ν->∞ then, as |υ|<c=1 => |υ |ν->0 and the above formula becomes:
![]()
This formula is identical to the classical relativistic, if the γ term changes as noted before. This formula has the same characteristics with the classical one, but the length is always a rational number. If υ=0, then the length is obviously an integer.
[5.18] the above formula is of course an approximation, it holds satisfactory for large ν. However, large ν means large υ and large L, i.e. velocities near c and macroscopic lengths. Consequently, it holds satisfactorily exactly in the area of Special Relativity.
[5.19] In really macroscopic distances, the Euclid’s norm replaces the quantum norm, so the sum of the ever declining terms can be replaced by an integral, just as Newton solved the Zeno’s paradox by replacing the infinite sum with an integral.
[5.20] This analysis of quantum Special Relativity will be completed with the metric. By the definition of the speed of light it holds:
![]()
As all observers agree on the speed of light, this equation is invariant in all changes of coordinates. This is no other than the quantum Minkowski metric for light (as usual ds=0). In macroscopic dimensions it can be replaced by the classical Minkowski metric.
It is easy to show that for u≠c the equation |ds| = |dt|-|dx|-|dy|-|dz| is also invariant.
6. General Relativity and Dark Matter
6.1 General Relativity
[6.1] Let an observer be at constant distance s from a point-like source of gravity. This source produces go quanta of gravity per quantum of time (by loosing of course an equal amount of quanta of energy).
[6.2] At an arbitrary distance r, as the quanta of gravity are being distributed at the quanta of space that exist on the surface of a sphere of radius r, the density of the quanta of gravity is g(r)= go/ΝΑ, where ΝΑ=3·2r, the amount of quanta of space on this surface (Eq. 1).
[6.3] If that source of gravity was not there, then the observer would count the distance s by sending a photon to be reflected and return after time τtotal= 2τ, where τ is the time needed for the photon to reach its destination.
As c=1 => s=τ= τtotal/2.
[6.4] If now at that point there is the above mentioned source of gravity, then the photon, while approaching the source, will have additionally to pass by some of the propagating quanta of space (i.e. the gravitons). Therefore, it will reach the source at a more distant time than before. The time needed for the photon to reach the source is:
![]()
When the photon is coming back, it moves parallel and with the same velocity as the quanta of gravity, therefore the time of this trip is equal to that of the case without any source of gravity. Consequently τ2=τ(s)
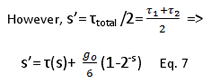
Conclusion: The distance that an observer counts inside a gravity field is larger than the corresponding distance in the absence of that source of gravity. In a way, the line has been curved.
[6.5] The corresponding relativistic equation (Schwarzschild) is:
s’=τ(s)+2mlogs , where m the mass of the source of gravity, expressed in meters.
One can observe that the term (1-2-s) increases with a decelerating speed, until it reaches go/6 at the limit s=∞ (Of course in a finite Universe s is always finite). As a consequence, it behaves like a logarithm (it does not tent to infinity but, after all, neither does the logarithm for finite s). This conclusion underlines the compatibility of this theory with General Relativity.
[6.6] The maximum value of the variable s in General Relativity as well as in this theory is naturally the radius of the Universe. If one sets s=R and then equals the “logarithmic” terms of the two expressions (and then sets (1-2-R)≈1) one finds:
go=12m·logR=12G·M·logR Eq. 8
Where M is the classical mass of the source.
[6.7]One can see that the amount of the produced quanta of gravity of a point-like source of gravity is proportional to the mass of that source. It follows that, like in General Relativity, also in this theory, the principle of Superposition holds for the first order terms. Thus, in the linear edition of the theory, the “curvature” that a source of mass Μ=Μ1+Μ2 produces, is equal to the sum of the curvatures that would be created by the masses M1 and M2 separately.
[6.8] As this theory is (at first order) equivalent to General Relativity for the problem of a point-like source and all the other mass distributions can be regarded to be a superposition of many point-like masses, one reaches the conclusion that the two theories are equivalent at first order for all possible distributions of matter!
[6.9] Of course the above conclusion holds only if the principle of superposition holds, i.e. if the existence of a second source of gravity near the first one would not change the amount of quanta of gravity the first source is producing. This is correct at first approach, but in general it is valid neither in GR nor in this theory, as one should take into account that the interaction of the two masses will increase entropy even further and so the amount of the producing quanta of gravity will increase.
[6.10] Eq. 8 states that the amount of quanta of gravity that a source of constant mass produces, depends (at first order logarithmically) on the radius of the Universe. However, by theorem 1.1 we have that this radius increases with time, therefore the same must be true for go. As a consequence, the gravitational force of a source of constant mass increases (very slowly) with time.
[6.11] In the next chapter we will analyze the inner mechanism of this increase and we will conclude that this mechanism is the so called Dark Matter and Energy.
6.2. Dark Matter
From paragraph [5.3] follows that gravity is produced by the increase of Entropy of the Universe, i.e. is produced when two bodies interact (we will not consider here how they interact). One might wonder: Where do these new quanta of gravity go?
The obvious answer is that they are heading towards some holes in the grid, i.e. some mathematically available points that are not covered already by a quantum of space. But how do these quanta of gravity know where such a hole exists?
Such information could only have come from the interaction that created these gravitons at the first place. For example, a quantum of gravity interacts with a photon, it transfers to it the information that there is a hole in the grid at the point (x,y,z) and afterwards that photon emits a graviton that heads towards the coordinates of that hole.
However, the interacting quantum of gravity, which inherited the information of that hole to its younger brother, might have get that information from another body, that might have get it from another, etc, in a long chain of interacting bodies, the first of which had actually passed near a hole and was thusly aware of its position. But what if at the time the last particle of that chain reaches the coordinates of that original hole, it finds out that the hole has been filled long ago by another quantum of gravity? In that case, the destination vector of that graviton will be identical to its position vector, therefore it will remain still.
[6.12] The above is a mechanism that has the unexpected conclusion that a graviton can stop, without becoming a quantum of space. As we will see, this is the mechanism of Dark Matter.
The following analysis will be separated into two cases:
Point-like source of gravity, constant in respect to Space:
[6.13] Let a source of gravity, constant in respect to Space, which as usual produces go quanta of gravity per quantum of time. For now go will be consider to be a constant. Let k(r) be the probability of a quantum of gravity to stop moving, after it has travelled distance r from its source. Then, at the surface of a sphere of radius r, k(r) go quanta of gravity will stop.
As k(r) is a probability, it must be normalized:
![]()
The specific distribution of this function is unknown, but at astronomical distances the integral
![]()
is expected to have a value around unity.
[6.14] The above considerations have two direct consequences:
First of all, a photon or a massive body, which moves towards the source of gravity, will notice a larger curvature of space than that expected from Eq. 7. Thus it will note that there is a halo around the source of gravity, whose size does not correspond to the mass of the source. This difference is usually named Dark Matter. Dark Matter is, sort of speech, stored gravitation from older moments of time in the Space around the source.
Second of all, as stated before, the amount of gravitons that a source produces depends on the number of interactions of the particles that consist the source. Therefore, if the density of quanta of gravity around the source increases, then statistically the interactions will also increase and thus go will not be constant any more.
[6.15] However, if that source of gravity is constant in respect to Space, then the density of stopped quanta of gravity inside a sphere of given radius will increase constantly with time. As a consequence, go always increases with time. But if go is an increasing function, then the expansion of Space around massive structures will also increase with time. Thus, the expansion of the Universe will also increase constantly. That is, basically, the mechanism of Dark Energy. This also explains the existence of a term depending on the radius of the Universe at Eq. 8. We will further analyze this fact at the next chapter.
[6.16] From the above it follows that, as go= go(t), inside a sphere of radius r and center the source of gravity, at every moment
![]()
quanta of gravity will stop.
[6.17] If at a moment to one has observe the density of stopped quanta of gravity around a source and have found it to be equal to ρο(to), then after time t, the average density of quanta of gravity (moving and stopped) around the source will be:

[6.18] At Eq. 10 the first term expresses the density of stopped quanta of energy at time to. The second term is the sum of gravitons that have stopped from to until to+t-r, divided by the amount of quanta of space of the sphere (thusly this term is also a density) and the third term contains all quanta of gravity (moving or stopped) that the source has produced the last r quanta of time. These gravitons have not yet left the sphere, so all of them are still inside it.
[6.19] For the equation of the derivative of go to be found, one needs a complete analysis of the way new gravitons are being produced by an interaction, but such an analysis is not in the goals of this paper. Nevertheless, instead of the exact formula, one could use the approximation of Eq. 8, i.e. go=12GM·log[R(t)].
[6.20]One observes that the increase rate of go is very slow, it depends on the order of magnitude of the radius of the Universe, which changes over billions of years. Therefore, one can consider go to be constant without an error, given that t is relatively small. In this case Eq. 10 gives:
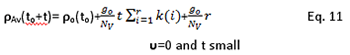
[6.21] In the study of gravitation, the average distances are almost completely astronomical. At such distances the discrete nature of Space is completely neglectable, so the macroscopic analysis can exchange the sums with integrals. Then Eq. 10 becomes:
![]()
With the same assumptions as at Eq. 11, the macroscopic average density is:
![]()
[6.22] General Relativity predicts only the third term. In that theory the curvature of a given source of gravity is constant and the density of stopped quanta of gravity is zero. These two terms are post-relativistic. The first term expresses Dark Matter and the second Dark Energy.
Equations of local density:
[6.23] The average density is very useful in order to find the expansion of a given length, as noted by an observer at distance r from the source (it is simply ρav·r), but for a complete analysis of this phenomenon one needs the density of quanta of gravity versus the distance r. For this case, the corresponding equation of local density is:
![]()
At a macroscopic level, the density of quanta of gravity versus the distance is:
![]()
Source of gravity with velocity υ in respect to Space
[6.24] Let a source of gravity, moving with velocity υ=(υ,0,0) in respect to Space, passing at time t from a point Ο. We will calculate the local density of quanta of gravity at a point A, in a 2-D example.
Let the source of gravity come from -∞. The distance of the source from A is (see Figure 3):
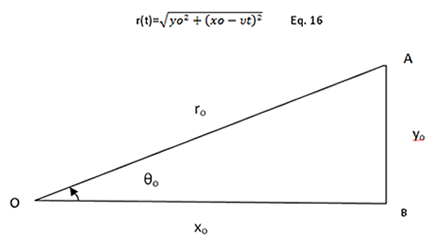 Figure 3: The initial distance of the source (at Ο≡-∞) from the point A(xo,yo).
Figure 3: The initial distance of the source (at Ο≡-∞) from the point A(xo,yo).
If the source passes from point B of minimum distance at time τ, then the density of quanta of gravity at the point A is:
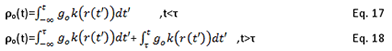
[6.25] One observes that when the source of gravity has a non-zero velocity in respect to Space, then the local density depends on the angle. The points that the source has already left behind have a larger density that those in front of it. Also, the larger the yo, the smaller the density. The density distribution has lost the spherical symmetry of the Eq. 15. It looks like the tail of a comet.
[6.26] The above observation leads to the capability of indirect measurement of the absolute velocity of a body: If a source of gravity has a spherically symmetric halo, then its velocity in respect to Space is relatively small. If its halo has a comet-like shape, then its absolute velocity is relatively big.
[6.27] The above conclusion seems to be in contrast with Special Relativity, but it is not. The observer has to “look outside the window” in order to find out whether he is moving in respect to Space or not. He cannot measure his absolute velocity by conducting some experiment inside his lab. The laws of nature will consequently be the same inside his lab, at any case.
7. Hubble’s Law and Dark Energy
[7.1] Let a galaxy that produces go quanta of gravity per quantum of time. Then a part of them will be stopping at various distances inside and around the galaxy, creating thusly phenomena of gravitational halos and expanding the space around the galaxy. If go is constant, then the space around the galaxy will be expanding with a constant speed.
[7.2] A photon from that distant galaxy that reaches an observer on Earth, has passed through a number of other galaxies. If these galaxies have an isotropic distribution, then their number will be proportional to the distance that light has to travel. If after some time a second photon from that distant galaxy is emitted, again at the direction of the observer, then at the meanwhile more quanta of gravity will have been stopped around these galaxies, therefore the same distance (observer-galaxy) will be denser; light will need more time to travel it. Moreover, light will interact with more quanta of gravity, therefore more of its quanta of energy will become gravitons, i.e. it will sustain a bigger red shift. Consequently, the observer will conclude that, that galaxy fended off.
[7.3] As the Expansion Ratio can be consider at first approach constant, the fending off ratio of the distant galaxies will be given by Hubble’s law[13]:
υ=Ηz Eq. 19
where z is the distance of the galaxies and H a constant.
[7.4] From equation 8 it should be clear that the number go of a galaxy is not constant, but it increases slowly with time. Therefore, the tempo with which quanta of gravity are being stopped around galaxies also increases. This increase of the expansion of the Universe is Dark Energy.
[7.5] This model explains the phenomena that have been connected with the existence of Dark Matter and Energy, without the ad hoc addition of any exotic structure.
8. Inflationary Universe
[8.1] One can argue that in today’s Universe the undergo expansion of a given length is not “real”, in the sense that there is no actual increase of the number of quanta of space that consist that length. Instead, there is an increasing amount of quanta of gravity moving around, making that length denser. That is so, because all possible holes in the grid inside what is called Visible Universe have been filled long ago. Thus, the increase of Entropy creates new quanta of gravity, which eventually have nowhere to go.
[8.2] However, in the distant pass, exactly after the Big Bang, the entire energy of the Universe was gathered into a very small volume, surrounded by infinite holes. At that time, when some ancient photons interacted, the newly created quanta of gravity had a very short distance to cover before they could turn into quanta of space. As the quanta of gravity were moving with the speed of light, at that time new space was created towards all directions with that speed too. At that first era, photons with enough energy to create several galaxies were moving towards the limits of the universe and they were, step by step, turned into space. This mechanism, which forced the ancient Universe to expand with the speed of light, it’s what is usually called: “the Inflationary Universe”[14][15].
[8.3] Of course at that time not all energy turned into Space. Some photons started interacting with each other and they created some massive structures, which had a smaller velocity than light. Thus, these structures could not reach the limits of the Universe, as its borders were moving away with the speed of light. From those massive bodies accrued all galaxies that are being observed today.
[8.4] When the photons that did participate in the Inflationary Expansion had turned completely into Space, that first era of the Universe ended. From that point on, new quanta of gravity were being created only in the core of the Universe, where there was still the residual energy of the ancient Universe. Between the core of the Universe and its borders there was a vast area of empty space, which made impossible for gravitons to interact with holes in the grid and find out their position. The core of the ancient Universe turned gradually into what is called “Visible Universe”.
9. Observable Predictions
[9.1] By using the conclusions of the last paragraphs, some easy-to-observe phenomena will be proposed, which are predicted only by this model, therefore they can be the judge of the truth (or not) of this theory.
1st Prediction: The halo of some stellar bodies has not a spherical symmetry, but a comet-like shape.
[9.2] The sole demand for the above statement, according to this theory, is the absolute velocity of that body not to be zero. One could easily assume that a heavy body (like a galaxy) is more likely to have a smaller absolute velocity, than a lighter body (like a star). After all, the lesser have a large rotation velocity around the galaxy, which means that they cannot possibly be invariant in respect to Space, as they are not inertial bodies.
[9.3] As a consequence, the 1st Prediction is expected to be applied on stars or equally massive bodies. For example, the space at the “tail” of the orbit of the Sun is expected to be more curved than at some point ahead of it. In other words, a satellite in orbit around the sun at a constant distance r, will count different radius return times of light, as that time depends on the angle its position constructs with the vector of the velocity of the Sun (in respect to the Galaxy). Of course this difference will be measurable, only when that satellite passes inside the tail of Sun. As this tail might not lie on the planetary plain, its direct observation might be difficult.
[9.4] The above prediction can be tested inside the Solar System. By using some already existing astronomical tables, another prediction can be tested:
2nd Prediction: If two stellar bodies (e.g. two galaxies) have with a good accuracy spherical halos, then these two bodies are expected to have very small absolute velocities, therefore they should also have an almost zero relative velocity.
[9.5] For the test of the last Prediction one should take into account the distance of these two galaxies from us. Due to Hubble’s Law, the more distant galaxies are seemed to move away, even though they are not. When the relative velocity of these two galaxies is being calculated, this fact should also be taken into account. An easy solution to this problem would be to compare velocities of galaxies that are roughly at the same distance from Earth. Thus the Doppler Effect will be equal in both cases; therefore it will not influence the relative velocity of these galaxies.
Conclusions
For the better understanding of the proposed model, it follows a qualitative interpretation of the evolution of the Universe, based on the above considerations.
At the Beginning, all the energy of the Universe was part of one gigantic photon. At the moment t=0, for unknown reasons, the Entropy of the Universe started to grow. As a consequence that photon started to break into smaller ones, which then were moving towards different points of the grid. A part of that titanic energy started to turn into quanta of space. Thus, the limits of the Universe were expanding with the speed of light towards all directions during that first era. This procedure kept going for a long time, until the Universe was split into two discrete zones: At the core there is an extensive zone (the so called Visible Universe) in which all the energy that has not already participated in the expansion of the Universe is stored. From the interaction of these photons were created all galaxies that one can observe. Outside that zone there is a vast empty space (which is so far away and so empty that cannot be seen) and at the limits of that area there are the physical boundaries of the Universe. If something goes near these boundaries, it will turn into space.
When these two zones split, the first era of the expansion of the Universe ended, the so called Inflationary. From that point on the expansion of the Visible Universe was not caused directly by the above mentioned mechanism, but only indirectly. That is so, because inside the ancient photons that finally created the Visible Universe there are still today information about the location of ancient holes in the grid. These locations can be very close, or even at the opposite sites of the Universe. Therefore, when two particles in the Visible Universe interact, they still create quanta of gravity, which moving towards the coordinates of those ancient holes.
During their propagation, these quanta of gravity act like additional moving space, in the sense that light and other bodies must cross them too. As a result, a given length inside the Visible Universe undergoes a pseudo-expansion, even though this expansion is not real, like the Inflationary. The Universe does not expand, only the travel time of light increases.
As a consequence of the above mechanism, some quanta of gravity reach at some moment the locations of the imaginary holes they were seeking. Naturally, inside the Visible Universe there are no holes. Thus, these particles stop moving, without becoming quanta of space. Due to this phenomenon gravitation of past times is stored inside the Visible Universe. As the gravitation caused by them can only increase, the density of quanta of space inside the visible Universe also increases, instead of staying constant, so the distances inside the Visible Universe grow.
Finally, the more the density of quanta of gravity grows, the more the number of interactions increases, therefore the more quanta of gravity are being produced. Consequently the expansion accelerates constantly.
From the above is obvious that the present model answers to all significant cosmological problems: Big Bang, Inflationary Universe, the Curvature of space-time, the red shifting of light, the phenomena of Dark Matter and Energy.
References
Special and General Relativity
1. Dirac P.A.M.: General theory of relativity, Whiley (1975)
2. Einstein, Albert: Relativity – The Special And General Theory, Methuen & Co (1916)
Accelerating Expansion
3. Riess, A. et al.: Astronomical Journal,116 (1998)
4. Perlmutter, S. et al.: Astronomical Journal, 517(1999)
Dark Energy
5. Peebles, P. J. E., Bharat Ratra: The cosmological constant and dark energy, Reviews of Modern Physics 75: 559–606. (2003).
Dark Matter
6. Hadley, Mark J: Classical Dark Matter (2007)
Loop Quantum Gravity
7. Smolin, Lee: Atoms of Space and Time, Scientific American (2003)
8. Smolin. Lee: Three roads to quantum gravity, Basic Books (2001)
Crystallography
9. Cornwell, J. F.: Group theory in Physics Vol. I, Academic Press (1984)
10. O’Keeffe, M., Hyde, B.G.: Crystal Structures; I. Patterns and Symmetry, Mineralogical Society of America (1996).
Photon’s condensation
11. Elesin, V. F., Levchenko, E. B.: Towards a theory of photon Bose condensation in nonequilibrium systems, Radiophysics and Quantum Electronics, Volume 22, Number 2, 88-95 (1979)
Entropy and Thermodynamics
12. Boltzmann, L.: Lectures on Gas Theory, University of California, Berkeley (1964)
Hubble’s Law
13. Hubble, Edwin, A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae, Proceedings of the National Academy of Sciences of the United States of America, Volume 15, Issue 3 (1929)
Inflationary Universe
14. Albrecht, A., Steinhardt, P., Turner, M., Wilczek, F., Reheating an Inflationary Universe, Phys. Rev. Lett., 48,1437 (1982)
15. Nanopoulos, D.V., et al. , Primordial inflation in simple supergravity , CERN, Geneva, Switzerland (1983)
Aris C. Chatzichristos is an undergraduate student of the Department of Electrical and Computer Engineering of National Technical University of Athens.
e-mail address: arishadj@gmail.com

Thank you very much for your help. I read the article very carefully and I think that it is, for sure, very interesting. I found some of its ideas fascinating, even thought I have serious doubts about some of its conclusions… Anyway, I am intrigued; I want to study the subject in more detail.
Thank you,
Best Regards,
Aris
Dear Dr Joseph Fine:
Thank you!
Warm regards,
A.R.
C. Aris,
http://www.workshops-hadronic-mechanics.org/isoshifts.html
I just received this abstract – or somewhat more than an abstract – on the wavelength shifts when light passes through a physical medium. I admit that I don’t understand a large part of this, while claiming to understand a somewhat smaller part. In any case, I am reading it several times. First, I think it is relevant, since several discussions here involve the cosmological redshifts et cetera. One might argue that empty space, which is not completely empty, is a physical medium itself and may contribute to redshifts. Then, add in the effect of gravity and the curvature of space and I am then outside of my competence. Nevertheless, I am bringing it to your attention as it may have something to add to your model. Please comment if you think there is something useful here.
Best regards,
Joseph Fine
Dear Argon,
Thank you very much for your encouraging words! Right now I’m working really hard to find my way through the minefield that is the Standard Model, pursuing these ideas and phenomena that might help me understand the other three Forces of Nature in terms of this discrete space-time model and such kind words give me strength to continue…
Since my last update I have many news, many leads and hints towards the direction of SM, but I won’t address them until I am definite about them. Right now I fell it is too early to talk about these ideas… I have still some very serious problems to solve, but I’m quite optimistic, I think I make progress every day…
Regarding your inquiry about a popularization form of this paper, I think that this is quite easy to be done. You see, in this paper there are no “abstract” things like a wavefunction or a spinor, everything is “tangible”. Thus, one can visualize the procedures in question, using for example the treadmill analogy, or other mind experiments… Moreover, If one follows this series of questions that I tried to address through my previous responses, one might find a detailed discussion of the most difficult, or interesting, parts of the theory. Thus, you can say that my answers are a fist attempt of popularize this paper.
Thank you very much,
Best Regards,
Aris Chatzichristos
Dear Mr Chatzichrístos,
Just wanted to let you now that please don’t let number of replies to your valuable post to mislead you. I really think that lack of comments is mostly because among us, readers of the blog, there are so few of those who could understand your theory. And way, way lesser who could start commenting on the subject.
Please keep up your important work and do like Mr Rossi: push on no matter what. You don’t necessarily even see what discoveries are waiting in path of your journey.
Do you have any news since your last update?
How would you explain gravity based on your thery for average reader?
In a hope of specialists on subject could help you with questions and comments.
Dear Mr Chatzichrístos,
sorry for my inattention and thank you for the reply.
Best wishes for your studies and researches.
Warm regards.
Dear GCV,
First of all, I am not a doctor. As stated at the end of the paper (after the “references” section) I am an undergraduate student. In NTUA (the University in which I am a student) the bachelor course is 5 years, and I have another full year until my graduation. Informally, the diploma given by NTUA is equivalent to a Master’s degree, but the bureaucrats still argue about it…
Anyway, indeed the tetrahedron is also a canonical polyhedron, but its shape differs even more from a sphere, than the cube used in this paper, that’s why I neglected it in my previous post. I remind you that Tommy proposed a shape that is closer to a sphere, than the cube and that’s how the canonical polyhedral came into the discussion. The thing is that it really does not matter all that much, what exactly the shape of the unitary cell of the grid is. In the end, all the various possible discrete geometries differ only by a multiplying factor. I used the cube, because the angles are 90o and thus it is easier to create a mental picture. Also, that’s what my Intuition says…
Thank you very much,
Best Regards,
Aris Chatzichristos
Dear Dr. Chatzichristos,
I wonder whether the Maldacena’s article about “The Illusion of Gravity” could be of some interest to you. One of the subtitles of the article says: “A quantum theory of gravity will probably provide us with an entirely new perspective on what spacetime is.”
The article is freely downloadable from here:
http://www.sns.ias.edu/~malda/sciam-maldacena-3a.pdf
Other papers by Maldacena are available here:
http://www.sns.ias.edu/~malda/PublicLectures.htm
Juan M. Maldacena is Professor at the Institute for Advanced Studies, Princeton.
http://www.sns.ias.edu/~malda/
Best regards.
Dear Dr. Chatzichristos,
I am aware that my question is marginal, but still:
why do you not include the tetrahedron among the “canonical” polyhedra?
http://en.wikipedia.org/wiki/Platonic_solid
Also, it seems to me that all its edges are equidistant from its center.
Wishing you the best.
King regards.
GCV
Dear Tommy,
Please bear in mind that only the nodes of the grid have a real meaning. There is no “between” these points in order to define your sphere. If you put a continius object (a cycle or a sphere) in a discrete geometry of course everything looks bizzare! But the idea of a cycle is an idealization, in a discrete geometry one can draw a cycle only aproximately, when r is large in respect to the quantum of space. The situation looks like what Archimedes did, in order to calculate the perimeter of a cycle…
As far as your idea of using polyhedra instead of “cubes” for the unitary cell, please recall that in 3D there are only four canonical polyhedra: Cybe, Octaedron, dodecaedron and eikosaedron. But, only the cube (I think) has the symmetry that all its edges are in the same distance from its center. In my opinion, this is the really important symmetry here, as the neighbouring points should all be at the same unitary distance. In any case, the use of another polyhedron whould not change the situation here and cybe is the simplest possible canonical polyhedron, thus it is preferred for simplicity reasons (Ocham’s razor). Anyway, if you choose another shape for the unitary cell, the geometry changes only by a constant factor, so I whould say it’s much ado about nothing…
I hope I answered your question satisfactory,
Best Regards,
Aris Chatzichristos
It seems to me that although you have introduced the 3 dimensional grid as a mathematical construct, it is manifested as a physical construct in the behaviors of the elements of the systems you describe, because outcomes depend on the orientation of the grid with respect to the direction of movement.
Imagine a circle with radius r. If I move parallel to the axis, it takes exactly r units of time to get to the circle’s border. If I move at 45 degrees, however, in r units of time, I am not at distance r, but rather I am at sqrt(5r^2/4) in classical units of distance. This shows an inhomogeneity in the grid that results in real consequences.
Please, clarify for me if I am missing something, but it does appear that the orientation of the grid would effect the movements of the particles in it.
Perhaps what you want is a construct where each cell is a 3 dimensional sphere. Imagine a die, with 6 surfaces. From any one surface, I can move to any four adjoint surfaces. If I were to add sides to the die and make each side indistinguishable from each other side, I’d create shapes like dodecahedrons, etc. As you can imagine, the more surfaces the die has, the closer each surface’s individual geometry becomes to a circle. Eventually, I’d construct something that would seem like a perfect 3d sphere, and on the surface, each individual surface would appear proportionally circular, and adjacent to each quasi-circle would be a finite set of homogeneous quasi-circles just like it, except that with respect to the third dimension each adjacent surface will be at an angle. By extending this concept to a four dimensional sphere, the three dimensional surface of that sphere could serve as a model for a fixed discrete grid of space that shows no preference for orientation with respect to the movement of its constituent particles.
Dear Joseph Fine,
Thank you very much for the links. I was not aware of the work of dr Drexler. I will study his theory carefully, as well as any other interesting idea that I come across.
Best Regards,
Aris Chatzichristos
Aris Chatzichristos,
Are you familiar with the “Post Modern” Cosmology arguments of Dr. Drexler?
Drexler’s idea is that relativistic protons are the basis of understanding the
nature of Dark matter. I recently learned of these ideas and thought they might “shed some light” on dark matter and dark energy, cosmic expansion and other cosmology concepts.
http://www.jeromedrexler.org/news/
http://www.jeromedrexler.org/a-relativistic-proton-dark-matter-would-be-evidence-the-big-bang-probably-satisfied-the-second-law-of-thermodynamics/
Joseph Fine
Good! Your open mind has earned a ticket to binary mechanics, where everything is quantized. Regards, j
Dear Tommy,
Thank you very much for your questions. I will try to answer them all:
If I wanted to model a universe evolution, I would first choose a finite integer E for the constant energy of that universe. Next, I would define E quanta. How might I constrain the vectors of each quanta at time zero to lead to interesting universes?
That is correct. The number E of the quanta of energy of the Universe is a (very large) ad hoc constant. One has to define its value manually, but of course its order of magnitude should be something like 10^100 (that is an educated guess).
At time 0, all quanta of energy were part of only one photon with position vector (0,0,0). Around that photon there was an infinite number of holes, but only the six neighboring holes could interact directly with the quanta of energy of the photon. Thus, the (1/6)th (statistically) of the E quanta of energy interacted with each hole, the initial photon broke into 6 more or less equally energetic photons, which then moved to fill the six holes around them. Thus, at time 1 there was one quantum of space at (0,0,0), six more quanta of space around it and the rest of the energy of the universe separated into six photons. At that moment two things happened:
Fist of all, the quanta of energy of the six photons interacted with the holes that were now around them (at distance 2 from the initial point (0,0,0)), they broke into more photons, most of whom continue to propagate towards the four corners of the universe expanding its borders as they moving.
Second of all, these six photons started interacting with each other. Thus one portion of the energy of the six photons of time 1 did not acquired a vector of position from a hole, but from a fellow quantum of energy. These quanta of energy did not participate into the expansion of the Universe, they were, more or less, trapped inside it.
Of course in order for one to build an accurate model of the Universe according to this theory, one has to define also the interaction of the photons. I think I have solved this problem, but as it has not to do directly with gravity, I left it out for simplicity reasons.
Can I assign to more than one quantum the same destination vector?
Of course you can. It is possible, for example, for all the quanta of an entire photon to have the same destination vector.
Is it required that one of the quanta have a destination vector which is the 0 vector?
Well, if you mean that at the time of the Big Bang one quantum of energy stayed at the point 0, as a quantum of space, then yes.
What occurs when more than one quanta reach a hole simultaneously? Is there a preference for which one becomes a space and which one(s) continue propogating?
Then, one of them fills that hole and the rest of them continue their journey as a photon with slightly less energy. There is no way to define which of these quanta will be transformed into a quantum of space. As I mentioned in the paper as well, this theory is non deterministic.
If one quantum’s destination vector matches position, and the others do not, is it forced to become a quantum of space while the others continue? What if none of the quanta are destined for position p? What if more than one are?
Please bear in mind that while that photon of yours approaches that hole, it gradually interacts with it. Thus, even if initially no quanta of energy of that photon had as destination vector the coordinates of that particular hole, some of them will eventually interact with it and change their destination vectors accordingly.
I was also unclear on the mechanism by which the presence of a graviton would effect the number of ticks it would take another particle in its vicinity to move. The analogy of the treadmill makes sense, but if there are no holes near the graviton, then presumably it is traveling on existing space and therefore does not create any new space in the local area across which the photon must traverse.
Well, you are absolutely right here. As you might have guessed, this paper does not contain the whole theory; it consists merely by the parts of it that have to do with gravitation. In this sense, I tried to simplify things when I could and by-pass some parts that would need a very extensive interpretation. For example I did not defined in this paper how the quanta of energy interact with each other. If I had, I could show you directly that when a propagating photon reaches a quantum of gravity, then it stops for a quantum of time and then continue its motion. Instead of talking in detail about these mechanisms, that might be very confusing without a detailed interpretation, I stated the treadmill analogy. It can be proven equivalent and it is easy to understand, that’s why I used it. Of course, when the rest of the theory is ready, these parts will be clarified.
Thank you very much for your attention,
Best regards,
Aris Chatzichristos
If I wanted to model a universe evolution, I would first choose a finite integer E for the constant energy of that universe. Next, I would define E quanta. How might I constrain the vectors of each quanta at time zero to lead to interesting universes?
For example, imagine a universe with energy 2. Imagine next I constrain the position vector of all quanta at time 0 to be the zero vector (big bang). Next, I imagine an infinite field of potential destination vectors for each of the two quanta.
Can I assign to more than one quantum the same destination vector? Is it required that one of the quanta have a destination vector which is the 0 vector?
What occurs when more than one quanta reach a hole simultaneously? Is there a preference for which one becomes a space and which one(s) continue propogating? Imagine that 10 quanta appear at position p at the same time t, and prior to arrival, there were 0 quanta at that position. If one quantum’s destination vector matches position, and the others do not, is it forced to become a quantum of space while the others continue? What if none of the quanta are destined for position p? What if more than one are?
I was also unclear on the mechanism by which the presence of a graviton would effect the number of ticks it would take another particle in its vicinity to move. The analogy of the treadmill makes sense, but if there are no holes near the graviton, then presumably it is traveling on existing space and therefore does not create any new space in the local area across which the photon must traverse.
Very interesting model!
Thank You,
Tommy
http://www.workshops-hadronic-mechanics.org/
San Marino Workshop on Astrophysics and Cosmology
for Matter and Antimatter
September 5 to 9, 2011
SESSIONS ON MATTER
Review astrophysical data on cosmological and other redshifts, the assumption of the exact validity of special relativity throughout the universe with particular reference to Doppler’s shift law, and the consequential interpretation of the redshifts via universe expansion, acceleration of the expansion, big bang, dark matter, dark energy and other conjectures;
Review conceptual, axiomatic, mathematical theoretical and, above all, experimental evidence suggesting deviations from special relativity within physical media, with particular reference to measured deviations from the Doppler’s law, and the numerical representation of cosmological, galactic and other redshifts without universe expansion, acceleration of the expansion, big bang, dark matter, dark energy and other conjectures;
SESSIONS ON ANTIMATTER
Review the widespread belief that antimatter asteroids can be seen via the use of Sun light as it is the case for the detection of matter asteroid; show the lack of resolutory technical content of such a view due to the known inability of Einstein’s special and general relativity to provide any differentiation between neutral matter and antimatter.
Review recent predictions from theories specifically built for antimatter according to which Sun light is absorbed without refraction by antimatter asteroids. Since Earth has been apparently devastated in the past by antimatter asteroids (see the references quoted below), our current unresolved inability to detect antimatter asteroids constitutes a threat to mankind, thus requiring serious collegial studies without aprioristic constraints, whether in favor or against Einstein’s doctrines.
Dear Janusz,
Thank you very much for your remark. When I checked again my calculations at first I felt really embarrassed about this trivial, obvious mistake of mine, but afterwards I found out that the correct formulas empower rather than weaken my conclusions. Nietzsche used to say that “Whatever does not kill you makes you stronger” and that is the case here, as the new calculations solve the one thing that was bugging me about my theory.
I will derive here the correct calculations:
2-D
In two dimensions, the retrospective formulae of Na is: Na(r+1)=Na(r)+4. It is very easy to find that in two dimensions Na(r)=4r
In order to find Nv one has to calculate the sum of Na(i) from i=1 to r. As Na(i)=4i, it follows that Nv(r)=2r^2+2r
3-D
The formula of Na in 3-D is a tricky one:
Moving along the z-axis, from z=-r+1 to z=r-1 (with the point of reference being at z=0), in every level with z=constant, the number of points that participate in the 3-D Na formula are equal to the number of 2-D Na(r-z)=4(r-z). At each of the levels z=-r and z=r there is only one point that participate in the 3-D Na formula.
From inspection:
for r=1 Na = 1+4+1=6
for r=2 Na = 1+4+8+4+1=18
for r-3 Na = 1+4+8+12+8+4+1=38
etc..
Thus, in 3-D, Na = 1+1+2Σ(4i)+4r. the sum is from i=1 to r-1
After the sum calculation, we have finally the correct formula for Na in 3-D:
Na = 4r^2+2
The above formula is needed only for the derivation of the very important Eq. 7 and 8. I have done the calculations using the correct formula for Na and the conclusion is the same, only the constant changes trivially. Thus, the qualitative conclusions of this paper remain unchanged.
On the other hand, the new formulas helped me overcome the sole remaining problem concerning this theory: As the norm used in this geometry is equivalent to Euclid’s, the two geometries should be equivalent. But that was not the case until now! With the false formulas I used, this was a very weak point of the theory. But one can see that with the new formulas, the number of points at the perimeter of a cycle is proportional to its radius, the # of points inside a cycle is proportional to the square of the radius etc. In other words, the important formulas of these two geometries are of the same order of magnitude, i.e. there are two constant numbers m and M for which: m*E<D<M*E ,where E and D are the formulas in Euclid’s geometry and in this Discrete geometry of the same thing (for example of the perimeter of the cycle with radius r).
I will correct the formulas in my paper and send the revised edition to replace this one. Hopefully there will be no problem.
Thank you very much for your remark,
Mea culpa
Best Regards,
Aris Chatzichristos
CHATZICHRISTOS ARIS:
Equations 1 and 2 are incorrect. By direct inspection, you can verify that for r=1, Na=6, for r=2, Na=18 (not 3*2^2 = 12 as per Eq. 1), for r=3, Na=38 (not 3*2^3=24 as per Eq. 1), for r=4, Na=66 (not 3*2^4=48). General formula is simple enough to derive–I leave it as an exercise.
Equation 2 can be similarly verified to be wrong.
Cannot comment on the rest of the article since this error discouraged me from continuing on reading.
Dear mr. Ernst
According to definitions 1.4 and 1.6, a quantum of energy is named “quantum of space”, when:
a)it does not move (its vectors of position and destination are identical) and b) it is a priori the only quantum of energy with a given vector of position.
At some point (x,y,z) there can be at some moment a quantum of space and additionally another quantum of energy. The second quantum of energy might be moving or not. Then, this second quantum of energy is named “quantum of gravity”. All in all, the difference is that a quantum of gravity is moving or standing still on some already existing space. In other words on a layer of standing quanta of energy. If a quantum of gravity finds a hole in the grid, then it “transforms” into a quantum of space and it stops moving. If it stops moving, without filling a hole, then it is not a quantum of space, it is a “stored” quantum of gravity, that will contribute to the “dark matter” halo of its source.
As far as your second question is concerned, you are right. A larger number of interactions between the two bodies will create a larger number of quanta of gravity, thus their gravitational strength will be (slightly) larger (of course, if you put a star near these bodies, they will be attracted much more to the sun, than to each other).
The above is not a new conclusion, it is valid also in General Relativity: The curvature created by two bodies, is larger than the sum of the two separated curvatures. In your example, the third body (either a star or a radiation source) will increase the curvature of the two bodies even further. The difference between GR and this theory of Discrete Space is that in GR this phenomenon can be mathematically predicted, but not physically explained. The physical interpretation of this phenomenon in my theory is the increase of interactions, as you have mentioned very well in your question.
Best Regards,
Aris Chatzichristos
Dear Mr Chatzichristos,
I’m still thinking about the way, in which gravitation is created in your model (probably in others too). Can quanta of energy be considered as quanta of gravitation or space at the same time or am I missing some point?
Imagine two asteroids in close distance, which emit nearly no energy (no fission, almost no radioactive emissions) and receive nearly no energy from e.g. suns, and most importantly, no cosmic radiation. Then these asteroids would (almost) not be attracted to each other. Now imagine, we suddenly put a sun in the vicinity of those asteroids or turn on cosmic radiation again, the asteroids would receive radiation, emit radiation again, quanta of energy would be moving between the asteroids, that would mean, they would attract themselves much more than before. Is that imagination correct, or am I missing the point again?
NOTE: In my last reply I wrote:
A quantum of energy contains one unit of energy(…) I do not know for sure how large this energy is (in eV for instance), but I suspect it to be equal to Plank’s Energy.
This is obviously wrong. Plank’s energy equals to 1.22 × 10^19 GeV, it cannot be the smallest possible energy!! This energy is the energy needed in order to observe a particle of volume equal to Plank’s volume (10^(-99) cm^3). If one quantum of space has volume equal to Plank’s, then its energy can be found using thermodynamics of Black holes. I am working on it at the moment.
Best Regards
Aris Chatzichristos
Dear mr. Ernst,
Thank you for your questions. I will try to address them:
You assume, that all quanta of space have the same unitary “size”, is there an ostensive reason for it, apart from making calculations much simpler?
There are two reasons for that: First of all, as you say, this is the siplest possible case. As the conclusions, followed by this hypothesis, contain Special Relativity, the Schwarzschild solution and some terms that migtht explain the phenomena previously connected to Dark Matter and Energy, there is simply no need to make things more complex. Thus, you can say that the first reason is “Ocham’s razor”: Between two equally good explanations, the simplest is preferable.
Second of all, in this paper, the quantum of energy is the only elementary particle. Space, quanta of gravity and photons (therefore also matter) are systems of an integer number of quanta of energy. One cannot find half a quantum of energy, just like in Democtitos’ theory one could not find half an atom (Ordinary atoms have an internal structure. Democritos’ atoms and quanta of energy have not). That is, after all, the definition of a truly elementary particle.
Do all quanta of space “contain” the same amount of energy (related to the unitary size)
Yes. A quantum of energy contains one unit of energy, i.e. the smallest possible energy. A photon consisted by three (for example) quanta of energy has of course energy 3. I do not know for sure how large this energy is (in eV for instance), but I suspect it to be equal to Plank’s Energy.
If so, what would happen, if a photon with higher energy hits a hole, will there a quantum of space be created and the remaining energy travelling on as a lower energy photon?
You are absolutely right. During this procedure one quantum of energy of the photon will become a quantum of space. Thus, if the photon had initially energy E (in quata of energy, where E is integer) after the procedure it will contain E-1 quanta of energy. As you can see at Chapter 8, this actual procedure was dominant during the Inflationary Era.
What if the energy of the photon is lower than the required energy, will the hole remain, waiting for a photon with higher energy?
In order for a hole to be filled, one quantum of energy is needed. A photon contains by definition at least two quanta of energy, while a graviton contains exactly one, therefore the photons have always the energy required to fill a hole.
Thank you very much,
Best regards,
Aris Chatzichristos
Nice theory, a few questions to the author:
You assume, that all quanta of space have the same unitary “size”, is there an ostensive reason for it, apart from making calculations much simpler?
Do all quanta of space “contain” the same amount of energy (related to the unitary size)?
If so, what would happen, if a photon with higher energy hits a hole, will there a quantum of space be created and the remaining energy travelling on as a lower energy photon? What if the energy of the photon is lower than the required energy, will the hole remain, waiting for a photon with higher energy?
Dear Enrico,
My response to your questions is the following:
The movement of massive and charged particles will be effected releasing energy in the space quanta?
Based on the above theoretical approach, all particles (charged or not) are stable systems of interacting photons (more details on this will appear into a new paper). As a consequence, the interactions of quanta of gravity with massive particles can de derived from the interaction of photons-gravitons. So, the answer to your question is definitely yes.
Charged particles could radiate energy when pass through deformed space like Bremsstrahlung radiation? Where we should expect these particles radiate?
Please forward directly to my e-mail the definition of “deformed space” in your question, in order to answer thoroughly. In any case, the above theory claims that space is getting deformed by the creation of new quanta of space, moving or steady, produced by the interaction of particles.
Measurement of such radiation will give some differences before or backword a moving massive object?
I tend to believe, based on the above approach, that the emitted radiation of a moving particle inside a gravitational field will be greater backwards, when the particle is decelerating and before it when it accelerates.
As far as the goals of the AMS-02 mission is concerned, I expect that no evidence of dark matter and dark energy will be observed. Moreover, the data collected by this device might allow us to test the second prediction of the above theory:
If two stellar bodies (e.g. two galaxies) have with a good accuracy spherical halos, then these two bodies are expected to have very small absolute velocities, therefore they should also have an almost zero relative velocity.
In general, the geometry of the halos of galaxies is expected to be spherical (when the absolute velocity of the galaxy is almost zero), american-foodball-like (when its absolute velocity is non zero, but relatively small) and comet-like (when the absolute velocity of the galaxy is large).
Thank you very much,
Best Regards
Aris Chatzichristos
Dear Aris,
may be it is too early, or may be not… i was thinking if you consider not only photons but also particles moving in this new theory of space-time. The movement of massive and charged particles will be effected releasing energy in the space quanta? Charged particles could radiate energy when pass throught deformed space like Bremsstrahlung radiation? Where we should expect these particles radiate? Measurement of such radiation will give some differences before o backword a moving massive object?
I ask you these questions because in 46 days the AMS02 particle detector will be part of the IIS (International Space Station) for the detection directly in the space of cosmic rays. This will open a new window in astrophysics and your theory could be give some usefull advice how to judge the results of measurements.
Enrico Billi
Dear mr. Mat Nieuwenhofen,
Dark energy was inserted into the Standard Paradigm in order to explain the acceleration of light’s redshift, not the redshift itself. Apart from that you are right:
I think indeed that light’s redshift is not due to Doppler’s effect. I think that light loses energy while inside a gravitational field because of its interactions with quanta of gravity, which produce new gravitons (i.e. moving new space). Those new particles can move away, or stop moving at some distance from their source. The first are responsible for all classical relativistic phenomena (curvature of space-time) and the latter for “dark matter” (they are of course neither “dark” nor “matter”. They simply are “stored gravitation”). The density of stopped quanta of gravity around masses can only increase (given that the bodies’ velocity in respect to space is relatively small), therefore statistically the number of interactions of light with quanta of gravity inside a given gravitational field will increase, thus the energy a photon loses while travelling a given distance increases with time. Consequently there is no need (according to this theory) for dark energy as well.
I hope this time I answered your question satisfactorily,
Best Regards,
Aris Chatzichristos
Dear mr. Thanasis Apostolou,
I am well aware of the Chaiting’s appoach (I read the “Omega” couple of years ago) and I must tell you that it was a relief for me to see that other people agree with my vision of the world… Even though my approach is based on the work of Zeno and Democritos, not of Chaiting, I consider him to be a great visionary of modern mathematics.
Give my best to Patra (unfortunately I cannot come for the carnaval)
Best Regards
Aris Chatzichristos
Dear mr. Lee Kwang
Thank you very much for both your kind words and your interesting question.
As you can see, through my paper I left in purpuse some unanswered questions, like: “How two photons interact?”,”What is mass?” etc… I think that answering those questions a road to Standard Model might open. I have already found a solution, with the EPR phenomenon playing a key role in it, which gives some very promising qualitative results. Anyway, I prefer “speaking with actions” so perhaps I will come back with another paper, when I finish the quantitative approach as well.
Best Regards,
Aris Chatzichristos
Dear mr. Chatzichristos,
Thank you for answering my questions. I formulated my second question somewhat unclear, so let me rephrase it.
The current cosmological models all are based on that the redshift (a real measurement) is caused by the doppler effect (an assumption). As far as I know up to now only Paul LaViolette had a alternate explanation, and I don’t know how good his theory is.
Your theory explains the redshift as not being caused by the doppler effect. Doesn’t this mean that because the whole basis of the cosmological model changes, there is no need to use ‘dark matter’ and ‘dark energy’ to explain the observations? After all, these were postulated because otherwise the observations could not be explained.
Regards, Mat Nieuwenhoven
Dear Mr Chatzichristos
Been mathematician reading your paper, the following of Gregory’s Chaiting approach on complexity theory “Metamath! The quest for Omega” came up to me immidiately:
Nevertheless, there are some intriguing hints that this particular universe may in fact be a discrete digital universe, not a continuous analog universe the way that most people would expect.
In fact these ideas actually go back to Democritus, who argued that matter must be discrete, and to Zeno, who even had the audacity to suggest that continuous space and time were self-contradictory impossibilities.
Through the years I’ve noticed many times, as an armchair physicist, places where physical calculations diverge to infinity at extremely small distances. Physicists are adept at not asking the wrong question, one that gives an infinite answer. But I’m a mathematician, and each time I would wonder if Nature wasn’t really trying to tell something, namely that real numbers and continuity are a sham, and that infinitesimally small distances do not exist!
Is it posible to have any comments of yours on the above Chaitin’s sugestion to “degitize physics”?
Regards from Patras
T. Apostolou
Dear Mr Aris
Given that your theory allows gravitation to rise from a complete quantum approach, making Relativity compatible with the theories of Quantum Mechanics, would we expect a modified Standard Model of QM that will not “collapse” due to gravitation? Can EPR be explained from this theory?
My congratulations for this enlighten paper
L. Kwang
Post Graduate in QM
Dear mr. Mat Nieuwenhoven,
In reference to your first question, the answere is that I am not certain. I study the “Pioneer anomaly” as well as other phenomena that might prove or disprove the theory stated above. It is too early to express any concrete results, yet.
As far as your second question is concerned, you are right. Inside the Visible Universe, I claim that a given distance does not really expand, it becomes denser and denser. Light loses energy during this process, i.e. its energy transforms into quanta of gravity. Thus, one does not need a new particle or an exotic structure to play the role of dark matter and energy. In this theory the phenomena traditionally connected to these concepts can be physically and mathematically explained without any other ad hoc assumptions: Dark Matter and Energy are being created by quanta of gravity “standing still” (i.e. by gravitation stored from past moments around masses).
Thank you very much for your questions,
Best Regards
Aris Chatzichristos
Mat,
The correct link is the same as yours, but without the parenthesis at the end.
http://en.wikipedia.org/wiki/Pioneer_anomaly
Anyway, this article briefly discusses MOND (Modified Newtonian Dynamics) as a potential (pun intended) explanation of this phenomenon.
Most readers would figure this out, but I wanted to save them the time.
J.F.
Dear mr. Chatzichristos,
as an interested layman I find your theory very interesting. Two questions if I may:
– Is your theory able to explain the ‘Pioneer anomaly'(see http://en.wikipedia.org/wiki/Pioneer_anomaly)
– Your theory gives a theoretical reason for light’s redshift, basically ‘tired light’. Doesn’t this mean that because redshift then isn’t caused by everything moving away, that the very need for dark Matter and Dark energy goes away?
Best of luck with your theory.
Regards, Mat Nieuwenhoven
Dear Joseph Fine,
As stated at paragraph [6.14], I believe that dark matter is just “stored gravitation from past times around massive structures”. In that sense, I agree with you and I believe that we will never observe directly the so called dark matter or energy, as they are merely “denser space”. The phenomena usually connected with the existence of these exotic structures (the stability of galaxies, the acceleration of the observed expansion of the Universe etc) can be explained, in my opinion, with the mechanism stated at 6.2.
Thank you for your question,
Best Regards
Aris Chatzichristos
If Milgrom is right and MOND (Modified Newtonian Dynamics) is correct, or more correct than POND (Plain Old Newtonian Dynamics), that suggests that the existence of Dark Matter is in jeopardy. I don’t have an opinion one way or the other on Dark Energy.
How does your theories of quantized space deal with the absence of dark matter and the evidence, so far, in support of MOND?
See:
http://news.sciencemag.org/sciencenow/2011/02/more-evidence-against-dark-matte.html
J.F.
Dear Dr Enrico Billi:
I agree perfectly with you.
Warm regards,
A.R.
This pubblication is very interesting. The history of science is full of true theories and ideas, but without proof they will be easy forgotten or denied by the major of science comunity. I hope i can read on this Journal of Nuclear Physics, or another one, the results of an experiment in order to proof if these predictions are right or not. In any way good luck
Dear Dr Stephan Klaus:
Thank you,
Warm Regards,
Andrea Rossi
Given the limitations of existing theories, this paper shows that the future is not so narrow as one would have expected. Not only have we witnessed through this journal that mainstream science has lagged behind its progress in light of the Rossi invention, but herein we read (with the existing document still missing some formulae) that an undergraduate student has tapped into the next frontier. It is high time that us old timers make way for the new generation to create our new future. It would certainly make Albert proud! Keep the music coming!
Stephan Klaus
81 year old physicist